生産関数と費用関数

単一財の生産者理論の章では費用関数は前提とされた．これは謎のブラックボックスである．100 万個作りたいと言ったら「200 億円かかります」とだけ言われるようなものである．この総費用関数はどこから出てくるのかが，この章の疑問となる．それを考えるために生産関数なるものを考えてみる．生産要素なるものを投入したら生産物が出てくる関数のことである．1 この生産関数から総費用関数を作るということをかんがえよう．

その生産要素とは何かといえば，財を作るために必要な材料，労力，機械などの資本などのことをいう．ここでは単純化のため，二つの要素，資本と労働によって財を生産できるものとしよう．資本の量を\(K\) (capital)2, 労働の量を\(L\) (labor)とする．

そして生産関数を\(f\)とする．つまり\(f(K,L)\)が資本と労働の組み合わせをそれぞれ\(K\)と\(L\)だけ投入した時にできる財の量である．

短期

さて，ではそれぞれどれだけ投入すべきかが問題になる．そのためにまずは，労働だけ調整できる場合を考えてみる．このように，一部の生産要素のみが調整できる状態のことを短期と呼ぶ．例えば，ケーキ屋は12月末に忙しくなるが，その度にケーキを作る機会を新たに購入したりしない．そんなことをすれば，暇なときに無駄になるからである．ではそういった時期にはどうするかというとアルバイトなどの人を増やしたりして対応する．ここでいう機械などが調整できない生産要素で助っ人で雇うアルバイトなどが調整できる生産要素である．ここでは労働が調整でき，資本が調整できないとしてみよう．ここでは\(K=\bar K\)の水準で固定されているとする．

ではこのような短期では財を\(q\)だけ作るにはどうしたら良いだろうか．これは\(q=f(\bar K,L)\)となるような\(L\)を考える．これを\(L^*(q,\bar K)\)と書いておく．こう書くのは\(q\)や\(\bar K\)によって必要な労働量が違うからである．機械がたくさんあれば，同じだけ作るにしても労働量は少なくて済むし，作るべき量がたくさんあれば，機械の量が同じでも労働量は多くなる． このときの費用はどうなるかといえば

\[C^{\text{短期},\bar K}(q)= w \cdot L^*(q,\bar K)+r\cdot \bar K\]

となる．ここで\(w\)は労働の価格で，\(r\)は資本の価格である．労働の価格は賃金率と呼ばれる．つまり時給みたいなものである．資本の価格はレンタル率と呼ばれる．イメージ的には機械を借りてきてそのレンタル料を払う感じである．多くの企業では機械はリース品（借りてきたもの）であることが多いという点を考えれば自然である．

さて，これで短期の費用関数を作ることができたわけである．ちなみに\( w \cdot L^*(q,\bar K)\)の部分が可変費用，\(r\cdot \bar K\)が固定費用となっていることに注意する．短期的に動かせないものが固定費用という扱いなのである．

長期

次に，労働も資本も調整できるような状況を考えよう．このような状況は長期と呼ばれる，すべての生産要素が調整できる世界である．このとき，\(q=f(K,L)\) を達成するような \(K,L\) の中で費用が最小になるものを考える．それを\(K^*(q),L^*(q)\)とすれば，総費用関数は

\[C^{\text{長期}}(q)= w \cdot L^*(q)+r\cdot K^*(q)\]

となる. \(K\)も動かせることに注意すること．

ではそのような費用を最小にする資本と労働はどのように決まるだろうか．実はこの発想は消費者の問題と全く同じである．生産量が同じになるような\((K,L)\)の組み合わせを結んだ曲線のことを等量曲線（あるいは等産出量曲線とも）呼ぶ．下記がその図である．

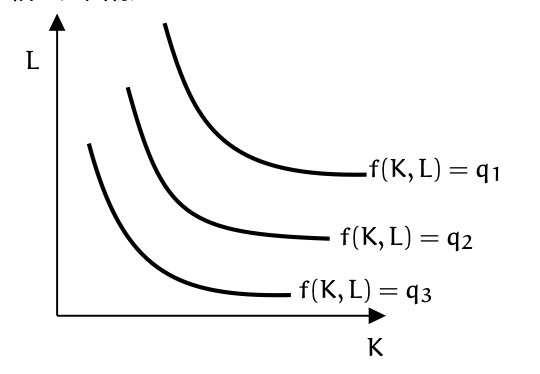
Fig. 33 等量曲線

この曲線の傾きは次のようにして求められる．\(\frac{\partial f(K,L)}{\partial K}\)を資本の限界生産物と呼ぶ．これは関数\(f\)を\(K\)で微分したものである これは他の生産要素の投入量が変わらないとき, 資本の投入量だけをほんの少し増やしたとき, 生産量がどれだけ増えるかを示している。労働の限界生産物も同じように定義する．

資本の労働に対する技術的限界代替率とは言葉の原義的には「資本をほんの少し(1だけ)増やしたとき，生産量を一定に保つためには労働をどれだけ減らしてよいかという交換比率」である。 減らすべき量を\(\Delta\)としよう。 すると，「増やした\(1\)が十分に小さければ」以下のような式が成り立つ。

\[\frac{\partial f(K,L)}{\partial K}-\frac{\partial f(K,L)}{\partial q_y}\Delta=0\]

したがってその交換比率 \(\Delta\)（技術的限界代替率）は以下のように計算できる。

\[\Delta = \frac{\frac{\partial f(K,L)}{\partial K}}{\frac{\partial f(K,L)}{\partial L}}\]

これは無差別曲線のときの話と同様に，等量曲線の傾き（の絶対値）と等しくなる．

これに対して，同じ費用を達成する\((K,L)\)の組み合わせを結んだ曲線のことを等費用曲線と呼ぶ．これは次の図で表される．

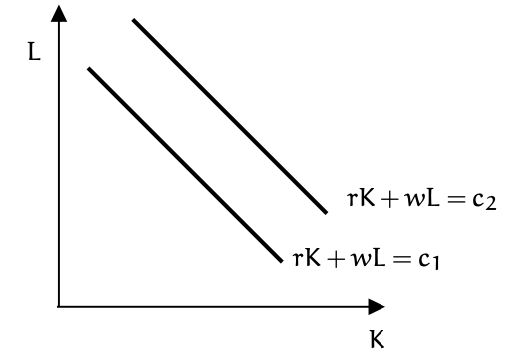
Fig. 34 等費用曲線

これは予算制約線とのときと同じで，生産要素の価格の比率\(r/w\)が傾きの絶対値になる．この等費用曲線は原点に向かっていけば行くほど費用が低くなる．

このとき，生産量を一定にしたもとで費用を最小にする\((K,L)\)の組み合わせは，次の図で表現される.

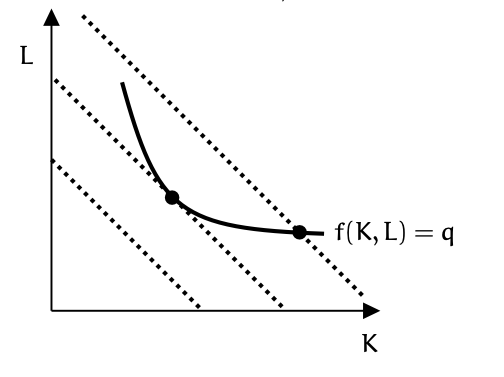
Fig. 35 費用最小化

つまり，等費用曲線と等量曲線が接するところである．もし，接しないとしたらどうだろうか．そもそも等量曲線上にない \((K,L)\) の組み合わせでは生産量 \(f(K,L)=q\) を達成できないので論外である．したがって，等量曲線の上の組み合わせを考える．もし等費用曲線と交わっているとしよう．そうすると，等量曲線が原点に向かって凸であれば，等費用曲線と等量曲線が交わる点が二つできる．すると，等量曲線は下に出っ張っているので，それよりもほんの少し低い費用を達成し，なおかつ等量曲線と交わる等費用曲線を描くことができる．そうであるなら元々の組み合わせでは費用は最小できていないことになるのである．したがって，費用を最小にするところでは等量曲線と等費用曲線は接することになる．

このようにして求まった\(K,L\)をそれぞれ\(K^*(q)\)と\(L^*(q)\)と書く．このベストな\(K,L\)はどれだけ作るのかによって変わる可能性があるので，その目印として\((q)\)をつけている．そうした\(K^*(q)\)と\(L^*(q)\)を用いると費用関数を\(C^\text{長期}(q)=w L^*(q)+rK^*(q)\)と求めることができる．

短期と長期の費用関数の関係

短期と長期の費用関数には\(C^{\text{短期},\bar K}(q)\ge C^\text{長期}(q)\)という関係がある．短期の資本の量\(\bar K\)は必ずしも適切な水準ではないので，それすらうまく変更できる長期と比べると，どうしても費用がかかってしまうのである．

例えば，ケーキ屋を考えてみよう．普段の状況（例えば5月とか）に合わせて道具や機械などを準備するならば，そんなに作る必要はないので，道具の量は最低限で良い．しかしその装備のままクリスマスを迎えてしまうと作る量が爆増するので，その分人を雇うか，大量に残業してもらうかして対応しなければならない．一方で，シーズンに合わせて道具や機械の量も調整できれば，そこまで人を雇う必要はなく，そのシーズンでの人件費込みでのトータルの費用は少なく済む3．

もちろん，たまたまベストな可能性もあるので，\(C^{\text{短期},\bar K}(q)= C^\text{長期}(q)\)となる可能性があることには注意である．

---

1

結局これもブラックボックスじゃないか，と思われるかもしれない．しかしこれはデータなどを用いて逆算することもできる．この辺りは実証産業組織論という分野が詳しいので興味ある方は参照せよ．

2

capitalが資本であるが，頭文字cが費用のコスト(cost)と被るので，ドイツ語のKapitalで考える，マルクスの有名な著書，資本論はドイツ語でDas Kapital である．

3

シーズンごとにわざわざ道具の量など調整できない場合も多い．その場合は永遠の短期である．