純粋交換経済とエッジワースボックス#
さて、前節で学んだパレート効率性という道具を用いて市場の効率性を検証する. 単純化のために、この経済には二人の登場人物、レオンとケネスしかいないとしよう. 財の種類は二種類、財\(x\)と財\(y\)であるとしよう.レオンの財\(x\)の消費量を\(q_{Lx}\)、財\(y\)の消費量を\(q_{Ly}\)、ケネスの財\(x\)の消費量を\(q_{Kx}\)、財\(y\)の消費量を\(q_{Ky}\)であるとする. また単純化のため、企業は存在しないとする.その代わり、各消費者はそれぞれ財\(x\)と\(y\)を一定量保有しているとする.これを記号で\(e_{Kx}\)などと表現する.また、これを初期賦存量や初期保有量と呼ぶ.こう言った形の経済を純粋交換経済と呼ぶ.
純粋交換経済における均衡(市場均衡、完全競争均衡、あるいはワルラス均衡と呼ばれる)は次の通りに定義される.
各消費者は与えられた価格\(p_{x}, p_{y}\)と初期保有\(e\)のもと効用を最大化するように消費量\(q_{ix},q_{iy}\)を決める.ここで消費者\(i\)の予算制約は以下の通りである.
(3)#\[ p_{x}q_{ix}+p_{y}q_{iy}=p_{x}e_{ix}+p_{y}e_{iy}.\]各財の需要量の和は各財の初期保有量の和に等しい.つまり
(4)#\[\begin{split}q_{Lx}+q_{Kx}=e_{Lx}+e_{Kx}\\ q_{Ly}+q_{Ky}=e_{Ly}+e_{Ky}\end{split}\]
1の条件は与えられた価格\(p_x,p_y\)の下、各消費者\(i\)が初期保有\((e_{ix},e_{iy})\)を売って得たお金を所得とみなして効用最大化問題を解くということである.
2の条件は各財の需給が一致しているということである.ここでは供給量は初期保有量ということで(4)の右辺である.需要は(4)の左辺である.つまりはどれだけ消費したいかと言う量の合計量である.ここで,財\(x\)はその間で需給が一致し, 財\(y\)もその間で需給が一致していると言うことに注意である.
エッジワースボックス#
財の配分(各消費者がどの財をどれだけ消費するかの組)を図に表してみよう.二人の予算制約の図を以下のように合体させた図を作る. 二人の初期保有の点が一致するように合体させていることに注意する.二人が直面している価格が同じであれば,予算制約線も傾きが同じなのでぴったり一致する.
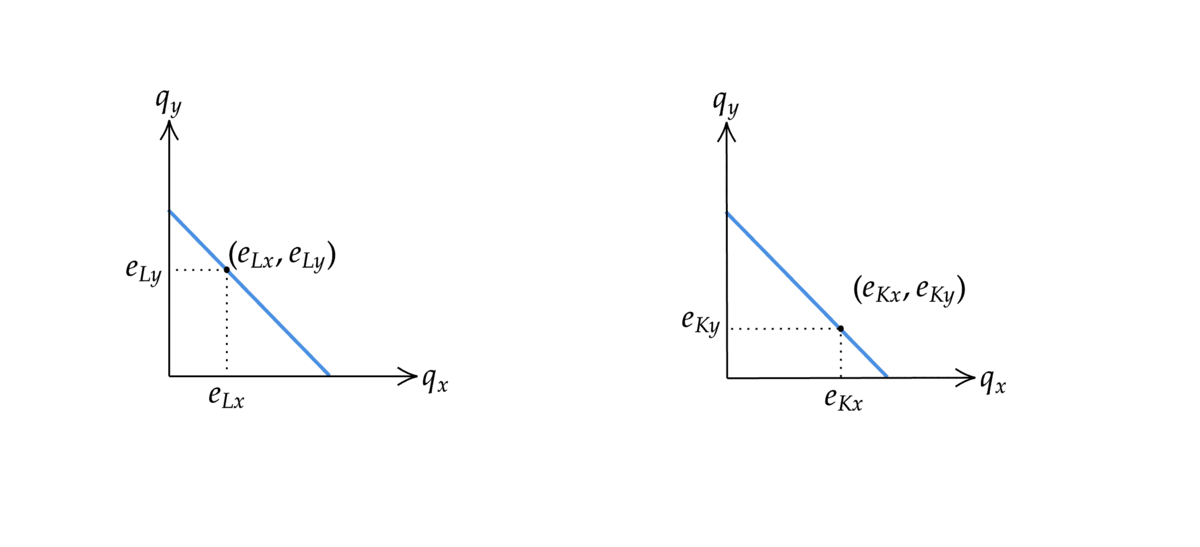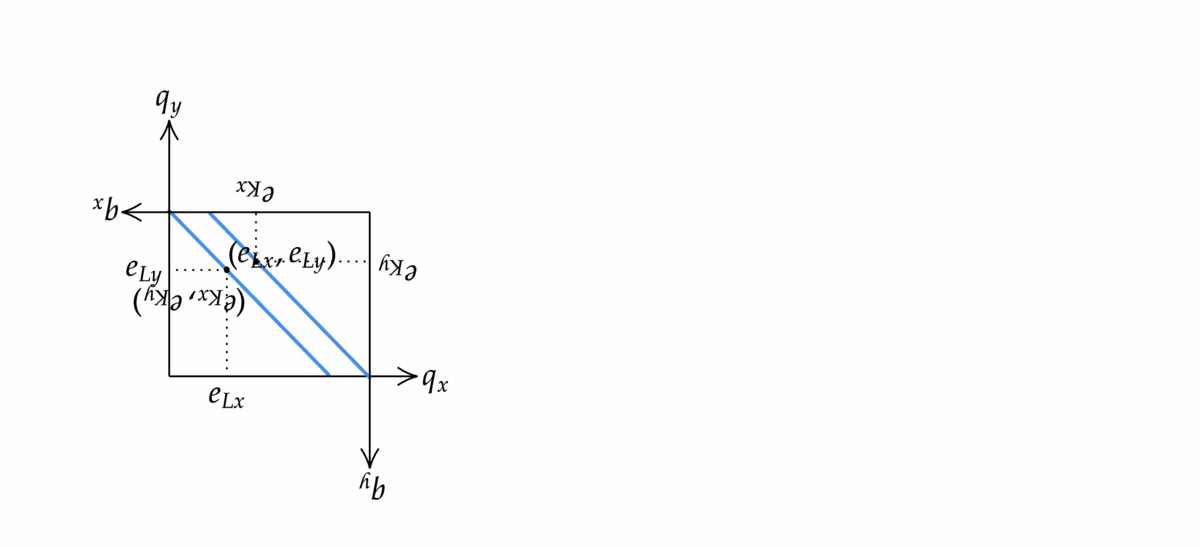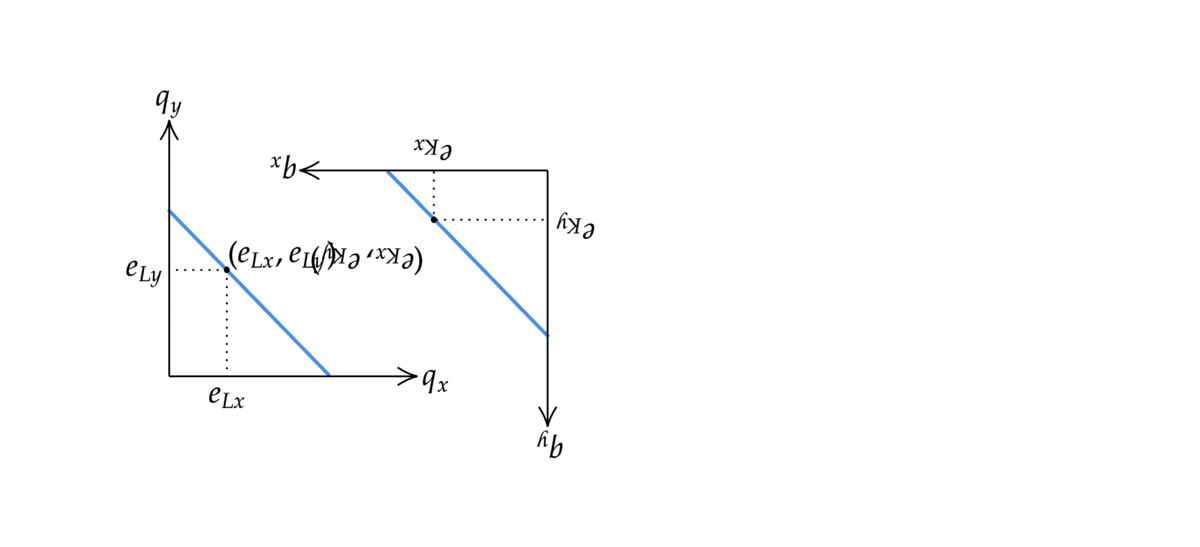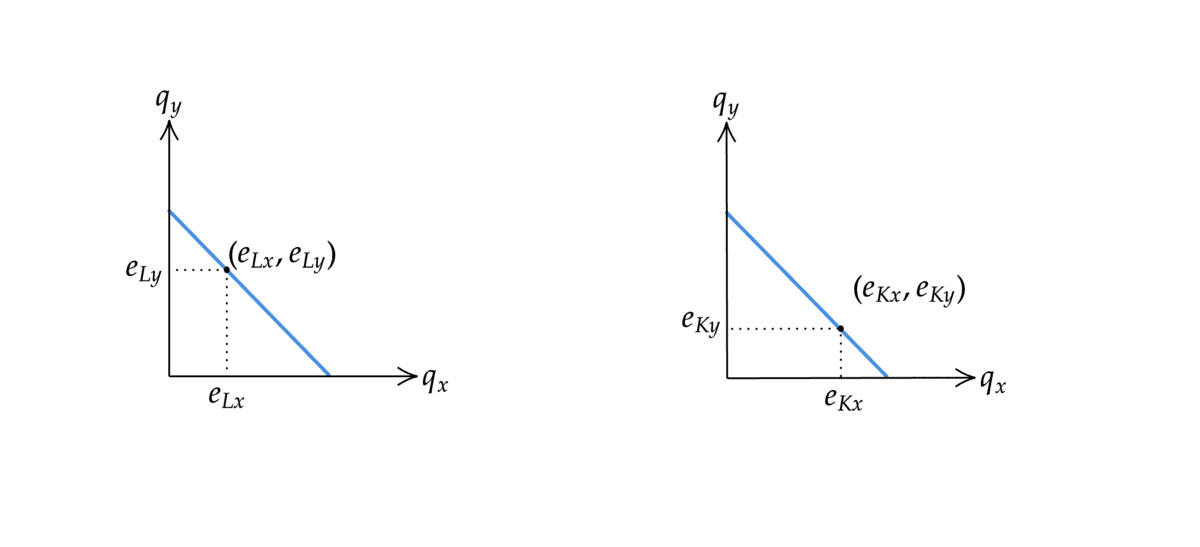
Fig. 36 エッジワースボックスの作り方#
こうして作られた図はエッジワースボックスと呼ばれる.
ちなみにエッジワース自身が描いたエッジワースボックスは現代のものと形が異なる.
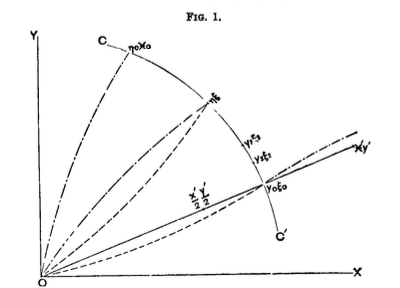
Fig. 37 エッジワースによるエッジワースボックス 出: Edgeworth, F. Y. (1881) Mathematical Psychics, C. Kegan Paul & Co.#
さて,エッジワースボックスが何を表しているかをみるためFig. 38を見てみよう.
Fig. 38 エッジワースボックス#
経済全体で消費できる財\(x\)の量は\(e_{Lx}+e_{Kx}\)であり、それは図の横軸で表されている.同様に経済全体で消費できる財\(y\)の量は\(e_{Ly}+e_{Ky}\)であり、それは図の縦軸で表されている. 点Aではレオンは財\(x\)を\(\tilde q_{x}\)だけ消費し、財\(y\)を\(\tilde q_{y}\)だけ消費する.一方ケネスはその残りの量を消費する.残りの量はちょうどケネスの消費空間の座標を回転させたもので対応できる.消費点Aは右上に行けば行くほどレオンの消費量が多くなるのに対し、ケネスの消費量はそれだけ少なくなる.
各消費者の消費量の組み合わせを配分と呼ぶ.要するに,ケネスとレオンの各財の消費プランの組み合わせ\((q_{Kx}, q_{Ky},q_{Lx}, q_{Ly})\)のことである.以下ではパレート効率的な配分やワルラス均衡における配分がどのような性質を持つかということについて議論する.
厚生定理#
さて、エッジワースボックスをつかってパレート効率的な配分を描いてみよう.Fig. 39を見てみよう.図中の実線がレオンの無差別曲線で点線がケネスの無差別曲線である.レオンは右上に行けば行くほど効用が改善し、逆にケネスは左下に行けば行くほど効用が改善する.今、消費点Aを考える.この点はパレート効率的であろうか?
Fig. 39 パレート効率的な配分#
点Aは残念ながらパレート効率的ではない.点Cと比較してみよう.点CではケネスにとってはAより良い.Aを通るケネスの無差別曲線より左下側にあるからだ.レオンにとってはどうだろうか.これもCの方が良い.Aを通るレオンの無差別曲線よりも点Cは右上側にあるからである.したがって点AからCに移動すればレオンとケネス両方の効用を改善することができる.これは点Aがパレート効率であることに反する.
では点Bはどうだろうか.点Bでは無差別曲線同士が接している.この場合、レオンの効用を改善する領域とケネスの効用を改善する領域が重ならない.そうしたとき、両者の効用を同時に改善するような点を見つけることはできない.したがって点Bはパレート効率的な配分である.
パレート効率的な配分自体は無数にある.パレート効率的な配分を結んだ曲線を消費契約曲線という.
さて、パレート効率的な配分と市場均衡における配分の関係を見ていこう.実際には次の二つの定理が成り立つ.1
第一厚生定理 市場均衡配分はパレート効率的である.
第一厚生定理は市場均衡の効率性を示している.市場に任せていれば自然にパレート効率的な配分に行き着くので外野は何もする必要がないというものである.この定理の成立をエッジワースボックスをつかって確かめてみよう.Fig. 40を見てみる.
まず、初期保有の配分(図中のE)と市場均衡の配分(図中のQ)は同じ予算線上にあることに注意する.まず、初期保有を売って得たお金が所得であるので、その所得で初期保有の分をいつでも買い戻せることに注意する.また市場均衡では各人の効用が最大化されているので予算を使い尽くすはずである.したがって各人の予算制約の上に消費点がある.
レオンは点Qを通る予算線で効用最大化を行う.したがって、点Qで彼の無差別曲線(図中の赤実線)と予算線は接している. ケネスも同様である.点Qにおいて彼の無差別曲線(図中の青点線)と予算線が接している.レオンとケネスの予算線は共通である.なぜならば初期保有の配分と市場均衡の配分を通る直線はただひとつしかないからである.したがって彼らの無差別曲線は共通の予算線を通じてお互いに接している.これは配分がパレート効率的であるための条件であったので、点Qはパレート効率的であることが確認できた.
Fig. 40 第一厚生定理#
これを動画でも確認してみよう.
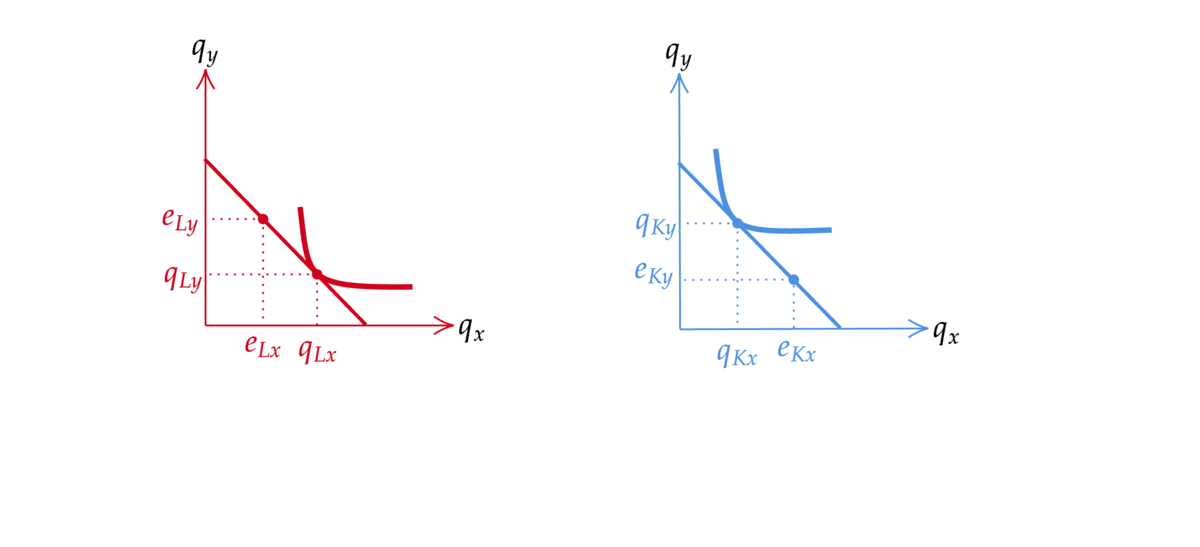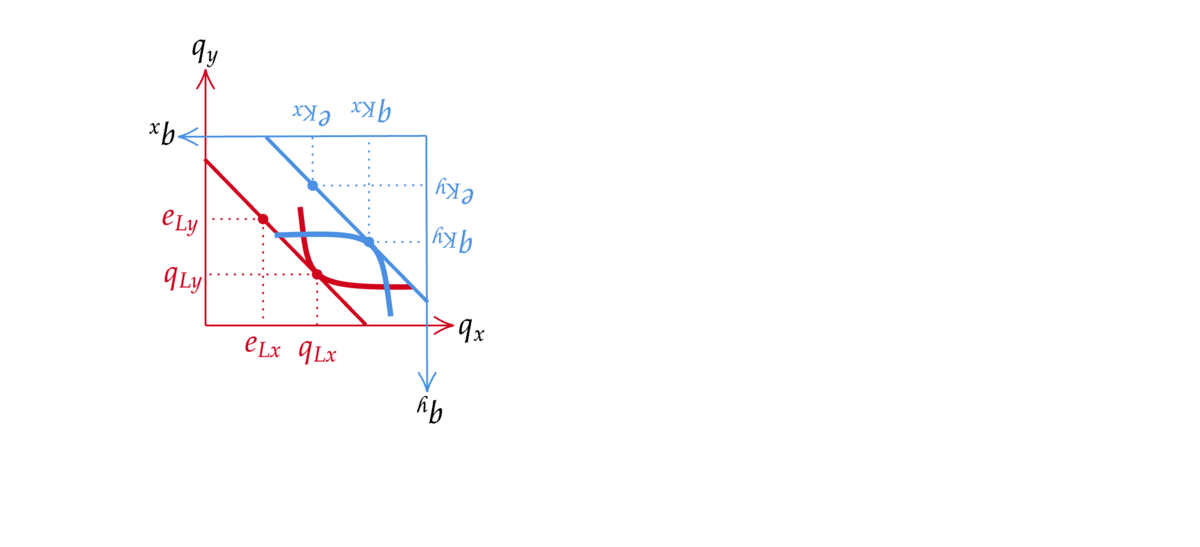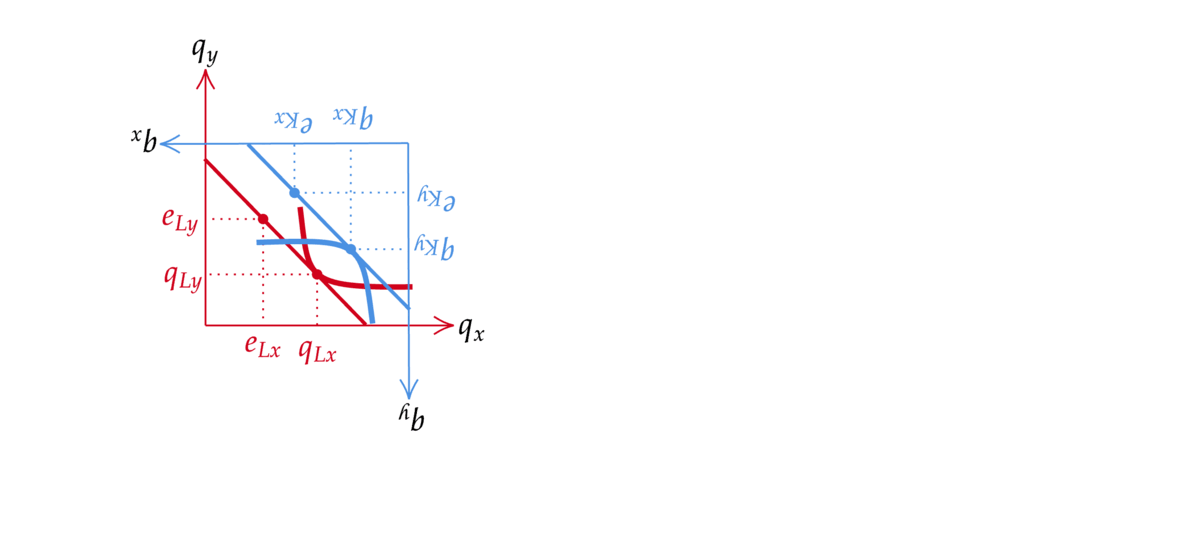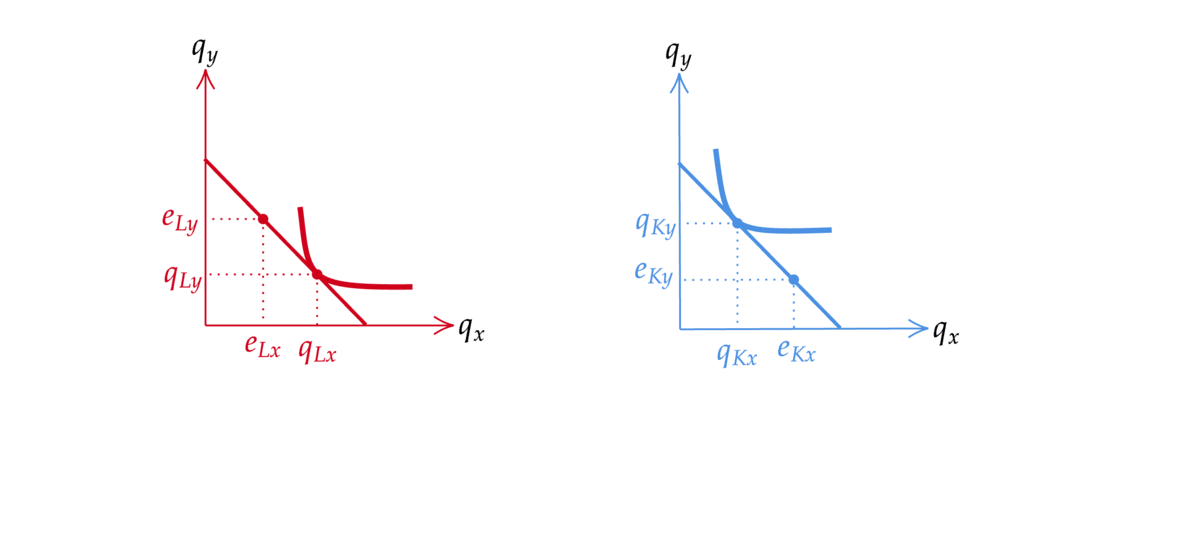
Fig. 41 第一厚生定理の動画による図解#
第一厚生定理とは逆に任意のパレート効率的な点を市場均衡を通じて達成することができる.これは第二厚生定理と呼ばれる.
第二厚生定理 パレート効率的な配分(のほとんど)は初期保有量を調整することで市場均衡を通じて達成できる.
これも図を使ってみてみよう.Fig. 42をみてみる.いまパレート効率的な点Qを適当に取ってくる.この点では両者の無差別曲線が接している. すると点Qを通り、二つの無差別曲線に同時に接する直線を描くことができる2.
この直線上の適当な点に初期保有の配分(点E)を通れば点Qが市場均衡の点になっている.
Fig. 42 第二厚生定理#
これも動画で確認してみよう.こう見ると第二厚生定理は第一厚生定理の逆再生とも言えるだろう.3
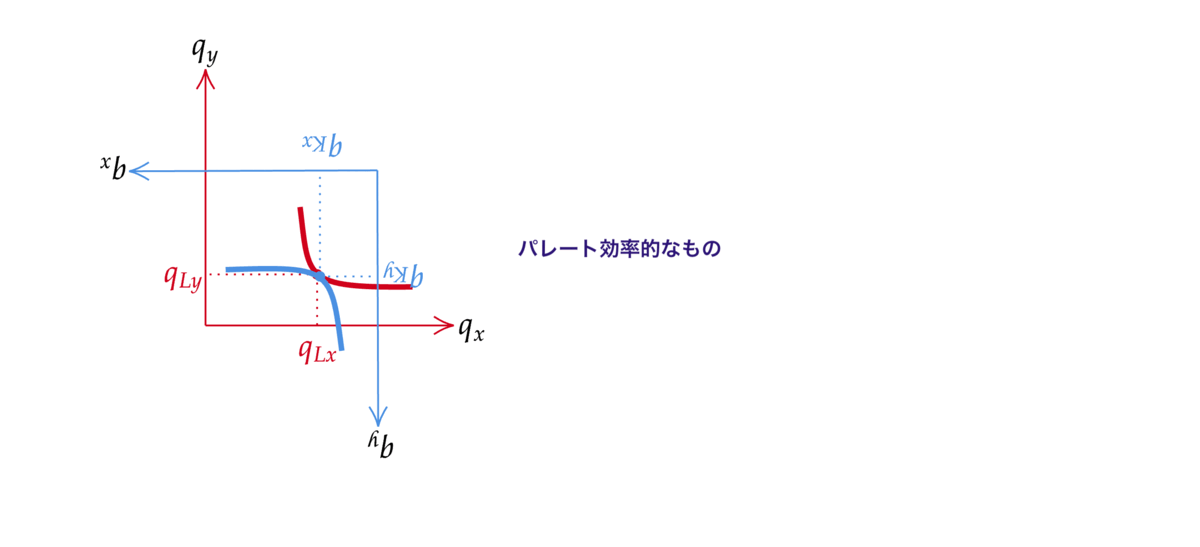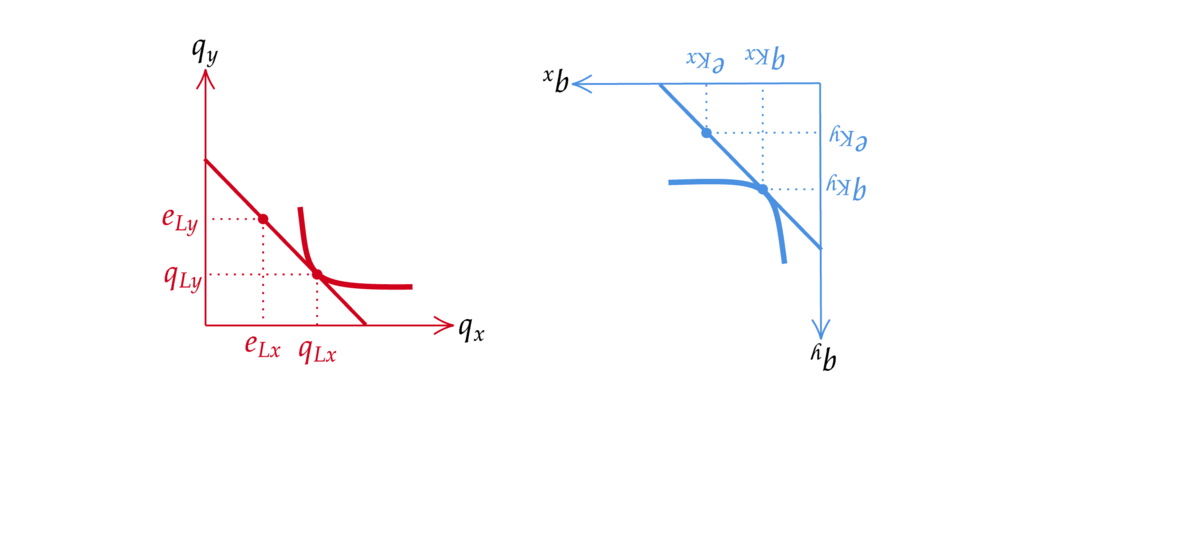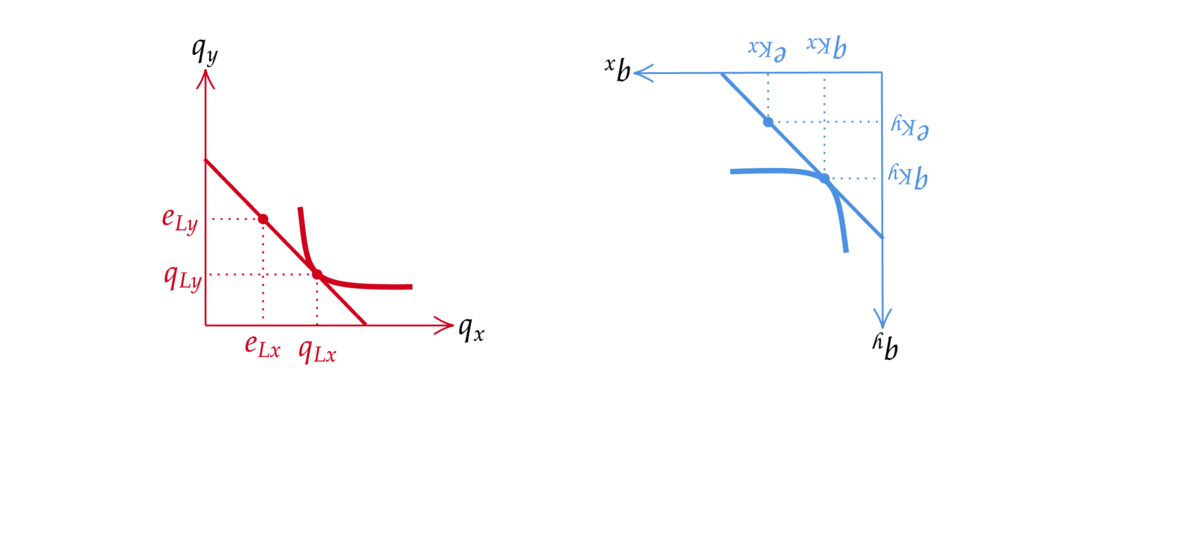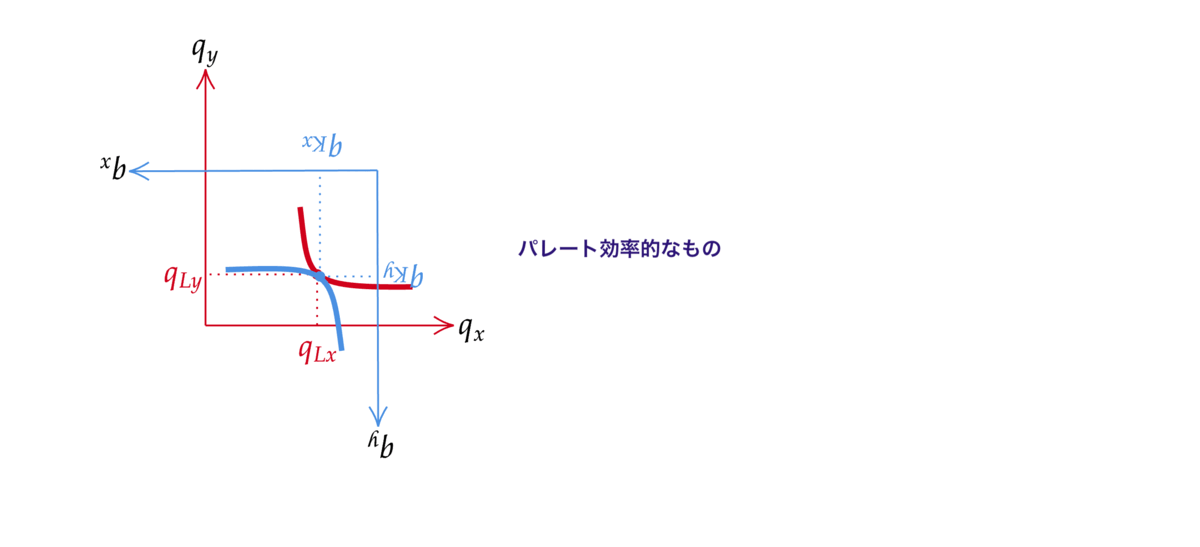
Fig. 43 第二厚生定理の動画による図解#
このように市場均衡とパレート効率的な点には密接な関係がある.
ただし,第二厚生定理が成立しないような例を作ることもできる.例えばFig. 44の中の点Aはパレート効率的であるが,どのように予算制約線を引いても市場均衡にはならない.財\(x\)の価格を0にすれば,A点で無差別曲線と予算制約線が接するようにできるが,そのときは財\(x\)を無限に買おうとしてしまうので,A点で効用最大化がなされない.
Fig. 44 第二厚生定理が成り立たない例#
厚生定理の注意すべき点としては,市場均衡の状態はパレート効率的であるが,市場均衡ではない配分から市場均衡に移動したとして,パレート改善するわけではないということである.
