市場における交換

具体的に次の状況を考えてみよう．ここでは「家」の市場を考えてみよう．この市場には家を欲しがっている人々と、家を建てることができる人々（大工）がいる．登場人物はTable 2のとおりである．上段が家が欲しい人、つまりこの市場では買い手となる人々である．彼らはそれぞれ支払意思額を持っている．支払意思額とは家を一軒買うときに支払っても良いと考えている金額の上限である．一方下段は大工、つまりこの市場では売り手となる人々である．彼らは家を一軒建てるのにそれぞれ表にある費用がかかる．今、買い手は家は最大でも一軒までしか欲しくないと思っているし、売り手も一軒しか建てられないとしよう．このときどのように買い手と売り手を取引させれば良いだろうか？

Table 2 家の取引

家が欲しい人	天照	出雲	高木	月読	大和
支払意思額（万円）	5000	3500	2000	1000	800
大工	アダム	イヴ	ルツ	ヤコブ	ヨセフ
費用（万円）	4500	3200	1800	950	850

適当に自由に売り手と買い手を取引させてやればいいと思うかもしれない． 例えばTable 3のように売り手と買い手が出会ったらどうだろうか（このように取引相手を組み合わせることをマッチングという）．

Table 3 適当なマッチング

買い手	天照	出雲	高木	月読	大和
取引成立の可否	💖	💖	💖	💖	💔
売り手	アダム	イヴ	ルツ	ヤコブ	ヨセフ

このマッチングでは天照とアダムは取引できる．なぜなら天照の支払意思額は5000万円である一方、アダムは4500万円で家を建てられる．したがって、天照が5000万円から4500万円の間の金額を支払えば取引成立である．このときこの5000万円から4500万円を引いた額500万円を取引から得られる余剰と呼ぶ．天照が払う額を\(p\)万円とすれば天照は\(5000-p\)万円だけ得をしたと思うだろうし、アダムには\(p-4500\)万円の儲けが出る．天照が得をした分とアダムの儲けを合計した分が余剰である．そしてそれは\((5000-p)+(p-4500)=5000-4500=500\)万円である．同様にして他の３つの組もうまく取引ができる．しかし大和とヨセフは取引ができない．大和は800万円しか支払意思額がないのにも関わらず、ヨセフは家を建てるのに850万円かかるからである． さてこの取引で得られる余剰の合計は\(500+300+200+50=1050\)万円である．これを社会的総余剰と呼ぶ．

さて，こうしたマッチングはうまくいっているだろうか．ある視点ではそうかも知れない．このマッチングは取引件数を最大にしている．一方でこの取引に不満がある人がいる．ヨセフである．いまヨセフは次のような取引を天照に持ちかけたとしよう．「\(1000\)万円払ってくれたらアダムの代わりに僕が家を建ててあげるよ」． 天照がこの取引に応じてヨセフに\(1000\)万円払ったらどうだろうか．このとき天照の得した分は\(5000-1000=4000\)万円である．アダムと取引した場合には最大500万円であったのに対し、大幅増である．また、ヨセフにも利益がある．ヨセフはTable 3では取引できず、何の収入も得られなかったのに対し、今度の取引では150万円の儲けを手にすることができる．この二人の取引はメデタく成立する．

このような事が起きる原因はアダムが取引に参加していることである．彼は家を建てるのに4500万円もかかるという非常に非効率な大工である．彼が家を建てる代わりにヨセフというわずか850万円で効率的に家を建てられる大工が取引から押し出されているのである．

市場取引はこういったことから起きる非効率性を解決してくれる．では市場取引とはどういうものだろうか． これを考えるために次の図を考えてみよう．Fig. 1における階段状の曲線は買い手の支払意思額を「高い順」に左から並べたものである．この曲線は需要曲線と呼ばれる．

Fig. 1 需要曲線

これがなぜ需要曲線と呼ばれるのだろうか．これを考えるために「価格」というものを考える．例えば家の価格が3000万円だったとき、家を買うのは誰だろうか？答えは3000万円以上の支払意思額を持つ天照と出雲である．すると市場で売れるのは2軒ということになる． ここで図中の需要曲線と3000万円を指す直線の交点を見てみるとちょうど数量が2になっている．つまり需要曲線とはある適当な価格を決めたときと売れる数量の関係を描いたものと言える．そしてFig. 1の需要曲線がそれであることはわかるだろう．このときの買いたい量のことを需要量と呼ぶ．

売り手の方も考えてみよう．Fig. 2の階段状の曲線は供給曲線と呼ばれる．これは売り手の一軒あたりの建設費用を「安い順に」左から並べたものである．供給曲線とは「価格が与えられたとき、どれだけ財が売りに出されるか」ということを指し示す曲線である．さしあたり価格を3000万円としてみよう．すると、この供給曲線によると「3人の大工が売りたいと思っている」ということがわかる． このときの売りたい量のことを供給量と呼ぶ．

Fig. 2 供給曲線

この二つの曲線を用いて、市場での取引が行われる．Fig. 3を見てみよう．これは需要曲線と供給曲線を同じ図に描いたものである．この需要曲線と供給曲線が交わるところで市場価格が決定される．ここでの価格は均衡価格と呼ばれる．図で言えば2000万円から1800万円の間である．さてこの価格では需要量と供給量が一致している．このとき市場で取引が行われ、買い手は均衡価格でものを買い、売り手は均衡価格でものを売るのである．

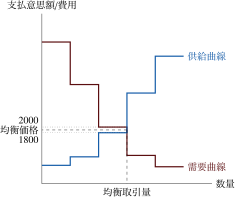
Fig. 3 市場均衡

さてこのとき、この取引で得られる余剰の大きさはいくらぐらいだろうか．仮に均衡価格が1900万円だったとしてみよう．この取引でものを買えるのは天照、出雲、高木の三人である．彼らの余剰の合計は\((5000-1900)+(3500-1900)+(2000-1900)=3100+1600+100=4800\)万円である．（買い手の余剰の合計を消費者余剰と呼ぶ．）一方で、この取引でものを売れるのは費用が低い順でヨセフ、ヤコブ、ルツの三人である．彼らの余剰の合計は\((1900-850)+(1900-950)+(1900-1800)=1050+950+100=2100\)万円である．（売り手の余剰の合計を生産者余剰と呼ぶ．）この二つの余剰を合計すれば社会的総余剰を計算することができる．そしてその値は\(4800+2100=6900\)万円である．Table 3の取引での余剰は950万円であったのでその差は歴然である．実は市場でのこのような取引方法は取引から得られる社会的総余剰を最大にする．そしてそれが市場における取引の利点である．

市場での取引に問題がないわけではない．市場での取引を見てみると取引成立件数がTable 3の取引では4件だったものが3件にまで減っている．これは非効率な売り手を排除した結果であるが、なにぶん不公平ではある．市場取引はこういった不公平感までは解消できない．したがって何らかの再分配などの措置がなされるべきであろう．

さてこの節では具体的な例を使って、市場の役割を見てきた．次節以降ではもっと一般的に市場の理論を展開していく．